小学校2年の娘ですが、自宅学習を怒られながら順調にこなしており、いつに間にか今は『くもんの小学ドリル 4年生のわり算』をやっています。先日やっていたのは2桁の割り算。この問題とてもよくできていると思うのですが、はたして問題の意図を理解できているでしょうか❓娘に確認してみましたが、反応は今ひとつ。。。思い起こせば、私もある時から出題者の意図を考えるようになり、算数がより楽しくなった記憶があります。どんな問題にも何らかの意図があるはずだという事で、私なりにこの問題の意図を考えてみたいと思います。
問題の法則性を見つける
では、早速問題を見ていきましょう。
①276÷91=
②276÷92=
③465÷92=
④465÷93=
まず①問目ですが、ざっくりと、270÷90くらいだと想像できますので、3で試してみると、答えは3あまり3となります。
続いて②問目です。こちらも同様に、270÷90くらいで、答えは3となります。
そして③問目です。465÷92=。割られる数字は変わりますが、大まかに450÷90くらいです。答えは5あまり5となります。
このような問いが続くのですが、少々怪しいですよね。え?怪しく見えない?いやいや、もう一度見てみましょう。数字の並びに規則性がありますよね。割られる数は同じ数が並び、割る数は1増えています。これが2つで1セットと考えられます。
どうです?段々と見えてきましたでしょ?最後に④問目も同じように、450÷90くらいで、答えは5となります。
まとめると以下のようになります。法則性は見えますか?
①276÷91=3あまり3
②276÷92=3
③465÷92=5あまり5
④465÷93=5

何だか数字が規則的に並んでいるね。3,3,3、5,5,5
こんな風に考えてみる
私が着目したのは、答えが「3あまり3」と「5あまり5」、それと割る数が1増えているところです。
3あまり3というのはどういう事でしょうか?①問目は276÷91ですから、276個を91人に分けると3個ずつになり、3個あまるということです。
つまり、3個のまとまりが91と3個のあまりが1ですので合計92のまとまりになると言える訳です。これが②問目の答えに繋がるのですが、お分かりのように③④も同様です。
では、もっと簡単な数字で考えたいと思いますが、ここでは「おはじき」で理解をしていきす。
・10÷4=2あまり2
・10÷5=2
早速、上記問題のおはじきの図を書いてみます。10個を4人に分けると以下の図のようになります。
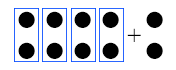
2個ずつのまとまりが4で、あまりのまとまりが1ありますね。つまり2個のまとまりは合計5です。これは次の問題の10÷5=2に繋がります。
答え(2)とあまり(2)が同じ数字になる場合、割る数が1増えると(4→5)、答えはあまりが0になります。
このように図で考えられるようになると、単なる数字の計算でなくなるので、定着も早いと思いますがいかがでしょうか。本人が理解できたかを確認するには、本人に説明させるのが良いと思います。「何故そうなったのか」を改めて言葉にすることで一層理解が深まることと思います。
ドリルをやるのは反復練習のためだ!早く解ければどうでもいい!という意見もあろうかと思いますし、それも正しいと思います。しかし、それよりも「算数は面白い」、「何故このような問題なのか」、という視点を持てるようにする事も大切なのだと思っています。

『算数面白い』ってお子さんが言ったら嬉しいですよね
わり算とかけ算の関係
かけ算まではスイスイ解けても、わり算になった途端に解けなくなった、というお子さんもいらっしゃると思います。何故わり算は分かりにくいのでしょうか。
計算を進めてみないと合っているか分からないから。(間違えるのが嫌だから)
これってたくさんの問題を解く時にストレスになりますよね。そう、手戻り覚悟で消しゴム片手にやるしかないからです。
先ほどの問題を例にとってみましょう。
465÷92=
大人であれば、暗算でこんな風に考えると思います。
『だいたい5だよね。5×90で450だから残りは15で、5×2で10だからあまりは5。』
しかし、この量感が無い子供たちは、とりあえず4くらいとか多分6くらいかな?などと、根拠なくやり始めてしまうかもしれません。これは非常にもったいないです。結局、計算をやり直すこととなってしまいます。
まずは、『90×5=450は超えていない、90×6=540は超えた。じゃあ5で始めよう!』というステップを頭の中で踏むようにして欲しいと思います。かけ算をしっかりやってきた子は数字を見ただけで、このあたりの勘が働くと思いますので、理解は早いと思います。
なにより、わり算ってなんだ?という事を本人なりに理解していることが大切です。
色々な考え方ができると思いますが、かけ算とわり算は表裏一体の関係ですので、四角形の面積と辺の長さの関係で説明をしても良いのかもしれません。
つまり、465÷92=でしたら、『1辺が92でもう1辺が5の長方形とあまり5』という具合です。このように考えると、どちらの辺を基準にするかで考え方が変わりますので、新たな発展が見られると思います。
今後、分数を勉強するときにも、わり算とかけ算の関係は意識せざるを得ませんので、今のうちにちょっとずつ種をまいておきましょう。




コメント